Aplicação de modelos alternativos para seleção de ações no mercado brasileiro
Autor: Helder Parra Palaro
Bayes Capital Management
Resumo
Foram examinados modelos alternativos de fatores de risco para construção de portfolio de ações brasileiras. Foram considerados 8 modelos lineares e 4 modelos não-lineares, e uma combinação de 4 modelos. Para portfolios long-only “LO” e long-biased “LB”, modelos como o IPCA (instrumented principal component analysis) e a combinação de modelos apresentam performance levemente superior e características de risco melhores do que o método tradicional de formação de portfolios por fatores de risco. Para portfolios long-short “LS” o método tradicional ainda é superior.
1. Introdução
A área de precificação de ativos tem como principal interesse explicar as razões pela qual diferentes ativos geram diferentes retornos.
O modelo CAPM foi introduzido independentemente por Sharpe (1964), Linter (1965) e Mossin (1966). Utilizando o paradigma de Markowitz (1952), o modelo assume que apenas um fator de risco é suficiente para capturar a diferença entre os retornos esperados dos ativos: o risco de mercado, que é o único risco sistemático, e portanto não-diversificável. Diferentes ativos possuem diferentes exposições ao risco de mercado. Esta exposição é capturada pelo coeficiente beta de cada ativo, que mede a covariância entre os retornos de cada ativo e os retornos do mercado.
Ross (1976) flexibilizou o conceito do modelo CAPM, assumindo que o retorno esperados dos ativos possam depender de não apenas um, mas de diversos fatores de risco. Neste caso são escolhidos como fatores de risco variáveis macroeconômicas de relevância ou características das empresas.
Fama e French (1993) formularam um modelo com 3 fatores de risco: risco de mercado, valor (medido pela razão entre valor patrimonial e valor de mercado) e tamanho da empresa. Carhart (1997) adicionou um quarto fator de risco, conhecido como momento, que depende de quanto a ação subiu ou caiu no ultimo ano. Estes métodos ordenam os ativos pelos fatores de risco, e criam assim carteiras long/short.
A busca por fatores de risco criou a situação descrita por Cochrane (2011) como “factor zoo”, onde centenas de características de empresas foram identificadas como influenciando retornos dos ativos. Porém muitas destas características possívelmente são proxys para mesmos fatores de risco, e portanto redundantes.
Kelly et al. (2019) propõe o modelo IPCA (instrumented principal component analysis) para precificação de ativos. Como nas abordagem tradicionais, os retornos esperados dos ativos são escritos como compensação por fatores de riscos não-diversificáveis. Porém estes fatores de riscos não são especificados à priori, mas são assumidos como latentes, e estimados por análise de componentes principais. As características das empresas são utilizadas como variáveis instrumentais na estimação dos betas de cada ação, que são um mapa entre os fatores de riscos e os retornos esperados.
Recentemente começaram a ser aplicados modelos de aprendizado de máquina para o problema de precificação de ativos. Modelos de aprendizado de máquina permitem tratar de maneira linear e não-linear dados com alta dimensionalidade, e utilizam métodos de regularização para evitar o overfitting.
Gu et al. (2020) examina diversos destes métodos para cerca de 30,000 ações individuais dos EUA. Os preditores são 94 características das empresas, assim como 74 variáveis “dummies” de setores, e 8 séries-temporais. Os resultados obtidos pelos autores mostram que modelos lineares têm boa performance quando penalização ou redução de dimensão é utilizada. Os modelos não-lineares melhoram a qualidade das previsões. Aprendizagem “rasa” funciona melhor do que aprendizagem “profunda”, onde o modelo tem várias camadas.
Gu et al. (2021) extendem o modelo IPCA de Kelly et al. (2019) para o caso não-linear, utilizando redes neurais conhecidas como auto-encoders para modelar a relação entre fatores de riscos e co-variáveis.
Rubesam (2019) aplica a abordagem similar à de Gu et al. (2020) para 572 ações do Mercado brasileiro no período de 2003-2018. São utilizadas 86 características das empresas. São formadas carteiras de acordo com métodos tradicionais long-short e ERC (Equal Risk Contribution). Os modelos não-lineares apresentam resultados decepcionantes. O método ERC que combina previsões de diversas técnicas de aprendizado de máquina produz os melhores resultados.
2. Métodos de aprendizado de máquina
Aprendizagem estatística e aprendizagem de máquina surgiram de áreas diferentes (estatística e ciência da computação), mas a distinção entre elas está cada vez mais difícil. Ambas focam em problemas de aprendizado supervisionados e não-supervisionados (Hastie et al. (2009)). No aprendizado supervisionado, que será a abordagem utilizada neste relatório, o objetivo é utilizar as variáveis independentes X1, X2, …, Xp (ou inputs) para predizer o valor da variável resposta y (ou output). Caso a variável y seja categórica, tem-se um problema de classificação. Caso ela seja continua, tem-se um problema de regressão. Iremos utilizar as duas classes de modelos. Deve-se então estimar uma função f, onde y = f(X | β). A função f depende de parâmetros β que devem ser estimados (treinamento do modelo).
O conjunto de dados (Xtrain,ytrain) utilizado para treinar o modelo é conhecido como dados de treinamento. Após o treinamento, temos a função de predição estimada fopt( | βopt). Então utiliza-se um novo conjunto de dados (Xtest,ytest) independente dos dados de treinamento, chamado de dados de teste. Pode-se então estimar ytest atráves de fopt(Xtest| βopt).
Existem também hiperparâmetros que controlam o processo de aprendizado através da complexidade do modelo. Um modelo muito complexo pode causar uma situação de ajuste redundante (overfitting), onde existe um bom ajuste aos dados de treinamento, mas não aos dados de teste. Por outro lado, um modelo muito simples pode não capturar todas as relações entre as variáveis.
O módelo mais simples considerado é o método de regressão linear múltipla. Este método assume que a variável resposta é uma função linear das variáveis independentes. Temos então y = Xβ, e não existem hiperparâmetros.
Os métodos de regressão Ridge e LASSO impõe uma penalização na estimação dos coeficientes da regressão linear, forçando os coeficientes para valores mais similares entre si. . A penalização é quadrática no caso de Ridge e em valores absolutos no caso de LASSO. Estas técnicas são chamadas de regularização. Elas reduzem a variância do modelo de forma significativa, introduzindo um certo viés. O hiperparâmetro controla a quantidade de penalização dos coeficientes.
Quando existem muitas variáveis independentes correlacionadas, uma alternativa é a redução de dimensão por componentes principais. Os métodos PCR e PLS utilizam esta técnica. No caso do PCR, o primeiro passo é criar novas variáveis Z1, Z2, …, Zm que são as combinações lineares de X1, X2, …, Xp que explicam a maior parte da variação dos dados originais, e são ortogonais entre si. Após isto, a variável resposta y é regredida nas variáveis Z ao invés das variáveis originais X. No caso de PLS, as combinações lineares são construídas com variáveis ortogonais também em relação a variável resposta y. O hiperparâmetro para estes métodos é o número de componentes principais.
O modelo IPCA também é um método linear que reduz a dimensionalidade do problema de estimação. Como especificado na introdução deste relatório, ele preserva a interpretabilidade dos retornos esperados dos ativos individuais como betas (factor loadings) multiplicados por fatores de riscos.
Iremos também considerar dois métodos lineares de classificação. O primeiro é a Regressão Logística, desenvolvida originalmente por Berkson (1944), que em sua forma mais simples utiliza a função logística para model um variável dependente binária. A segunda é a Análise Linear do Discriminante (em inglês LDA), de Fisher (1936). Neste modelo geramos funções discriminates, que são combinações lineares das variáveis independentes. O método assume normalidade multivariada, o que pode ser mais eficiente se esta suposição for válida, mas caso contrário a regressão logística é mais robusta.
O primeiro modelo não-linear a ser considerado são as florestas aleatórias. Árvores aleatórias (Breiman et al. (1984)) particionam o espaço amostral (valores possíveis de X1, X2, …, Xp) em diversas regiões disjuntas, onde a resposta é considerada como a média de y para esta região. Este particionamento é feito através de um algoritmo que determinada, a cada passo, uma variável e um ponto onde o espaço amostral será dividido. O número de partições determina a complexidade da árvore. As florestas aleatórias (Breiman (2001)) se baseiam na construção de um grande número de árvores aleatórias não-correlacionadas, e no próximo passo é calculada a média das respostas destas árvores. É uma aplicação da técnica estatística conhecida como bagging, onde a média de diversos preditores fracos (com alta variância mas sem viés) produz um preditor forte. O método de construir árvores não-correlacionadas é obter um subconjunto de tamanho m das p variáveis independentes, onde m <= p. Isto evita que uma variável, ou um número pequeno de variáveis, dominem a maioria das árvores que serão combinadas. Os hiperparâmetros são o nível de complexidade da árvore e o número m de variáveis a ser obtido para a construção de cada árvore.We also consider two linear classification methods. The first one is the Logistic Regression, originally modelled by Berkson (1944), which in its simplest form uses a logistic function to model a binary dependent variable. The second is the Linear Discriminant Analysis (LDA), from Fisher (1936). It generates discriminate functions, which are linear combinations of the independent variables. It assumes multivariate normality, which can be more efficient if this assumption holds, but otherwise the logistic regression is more robust.
Redes neurais são modelos não-lineares que compreendem uma ou mais camadas intermediárias (hidden layers) (Bishop (1995) e Ripley (1996)). Na primeira camada, são criadas novas variáveis Z1, Z2, …, Zm , definidas como Zi = σ(a0 + aitX), onde σ é chamada de função de ativação. Uma função de ativação comumente utilizada é a função sigmóide, dada por σ(x) = 1/(1+exp(-x)). Após isto, podemos ter novas camadas intermediárias, onde as variáveis da primeira camada são novamente combinadas. Finalmente, na última camada, temos as variáveis respostas à serem preditas. A estimação do modelo é feita por um algoritmo chamado de “backpropagation”. O hiperparâmetro controla a parada da otimização para evitar overfitting.
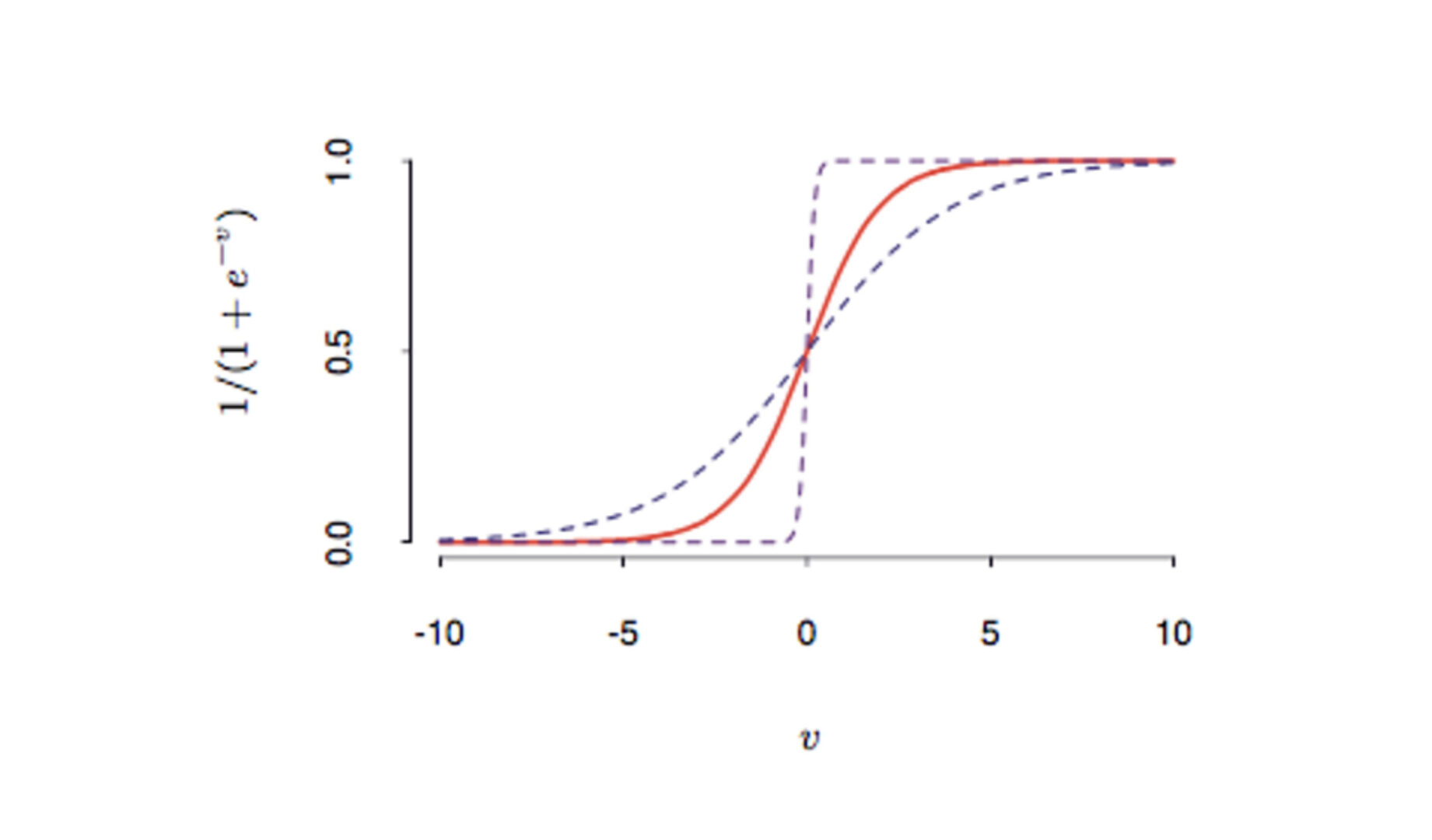
Figura 1: Exemplo de função sigmóide.
O último modelo considerado é um modelo de classificação, o modelo de Support Vector Machine (SVM). O método é descrito em detalhes em Vapnik (1996). Neste método construímos hiperplanos que maximizam a distância para dados de treinamento de qualquer classe. Para muitos conjuntos de dados, as classes não são linearmente separáveis, deste modo os dados originais são mapeados para uma dimensão maior ou mesmo infinita. Funções Kernel pode ser utilizadas para transformar o método em não-linear.
3. Dados
O conjunto de dados inclui 413 ações brasileiras no período Janeiro 2003-Julho 2021. Os retornos mensais de cada ação são calculados, e a cada mês utiliza-se apenas as ações que passam no filtro de liquidez (Figura (2)).
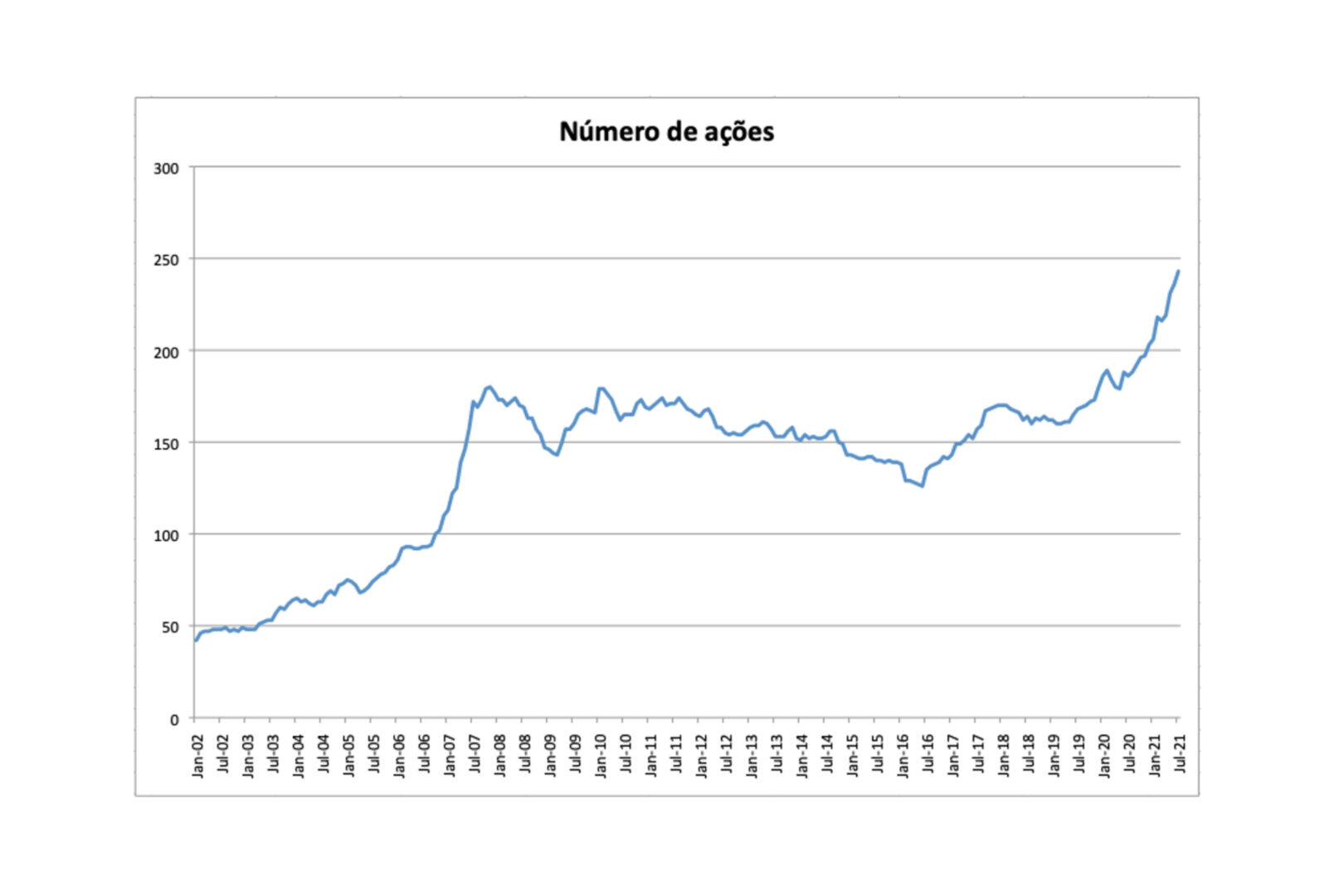
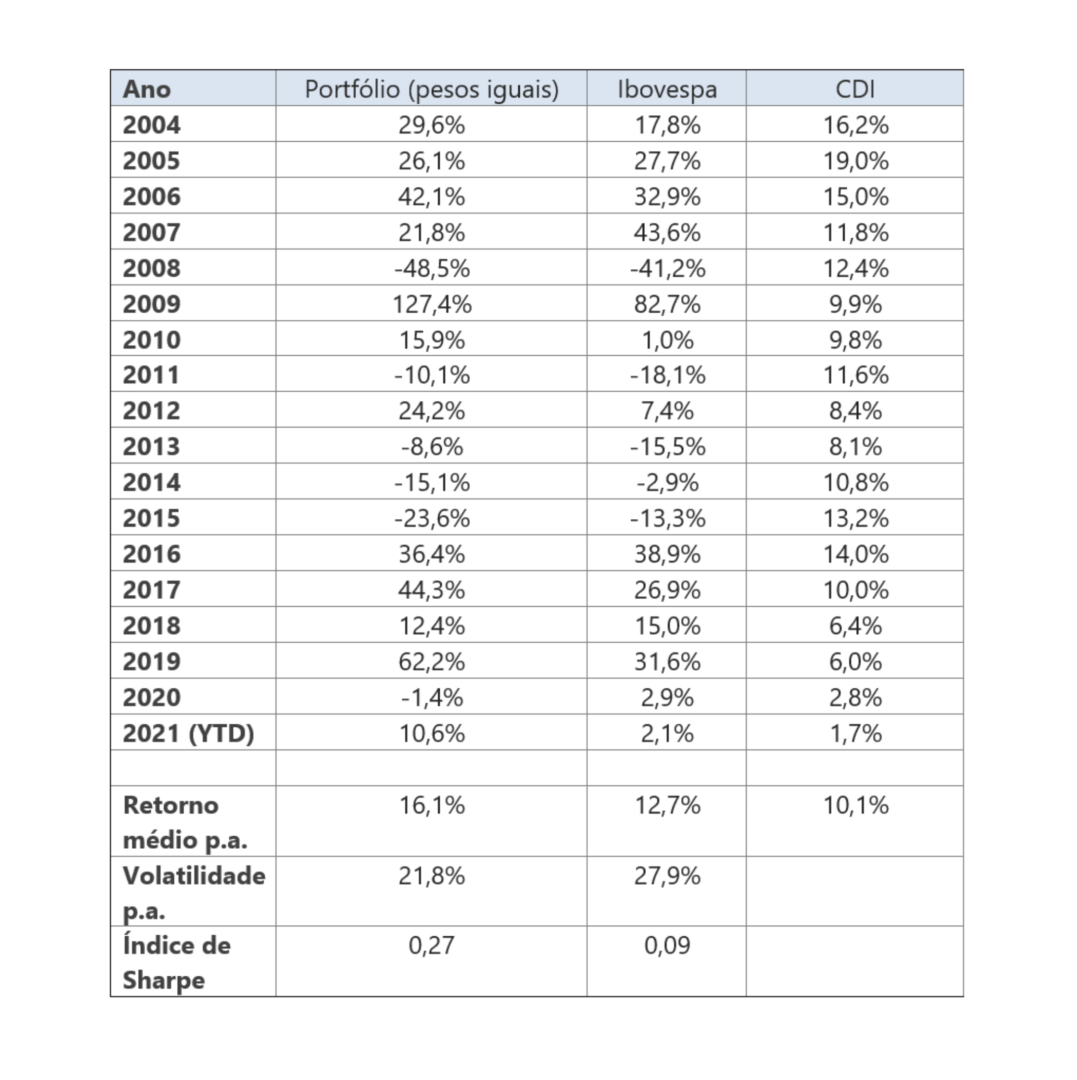
Construindo um portfolio com pesos iguais para cada ação que passa no filtro de liquidez1, são obtidos os resultados da Tabela 12. Nota-se que nosso universo de ações é mais diversificado, e tem performance melhor do que o indice Ibovespa, que é muito concentrado em alguns setores específicos.
1 Volume médio acima de R$ 200.000,00.
2 Em todo o relatório consideramos os custos típicos do mercado de ações, e rebalanceamento mensal.
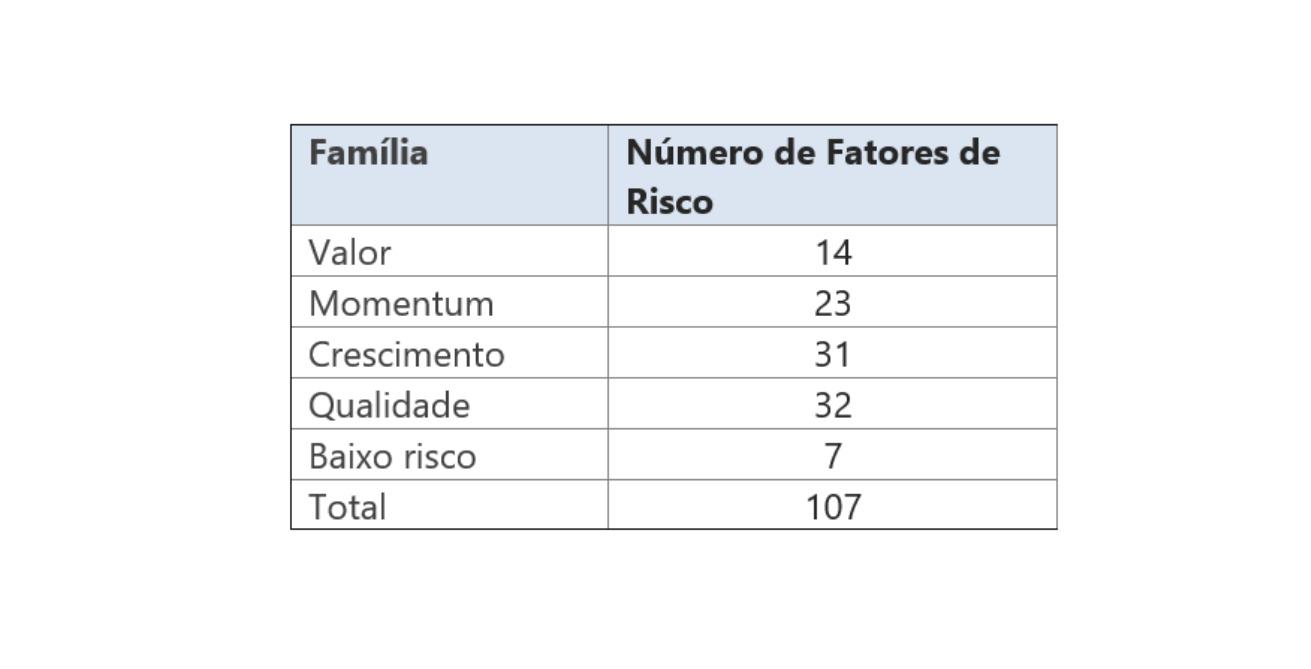
Além dos retornos mensais, o banco de dados, que vem sendo aperfeiçoado desde a primeira versão do modelo de fatores em 2012, compreende 107 indicadores técnicos e fundamentalistas para cada empresa. Este indicadores são criados à partir de dados de balanço e de dados de mercado, como preço, volume, liquidez, etc. De acordo com a introdução deste relatório, estes indicadores são chamados de fatores de risco. Estes fatores podem ser agrupados em 5 famílias de fatores de riscos, como descrito na Tabela 2.
4. Metodologia
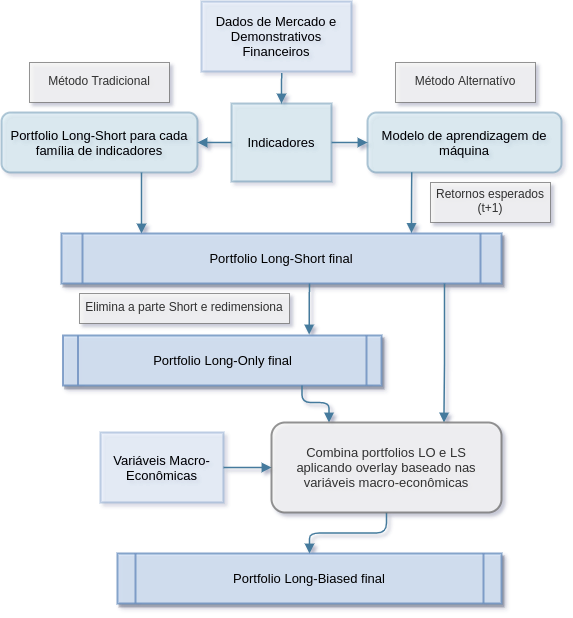
A Figura 3 exibe um diagrama do método de geração dos portfolios LS (long-short), LO (long-only) e LB (long-biased). Na primeira etapa, são gerados indicadores para todas as empresas do banco de dados. No método tradicional, estes indicadores são combinados por um processo proprietário para a criação de 5 portfolios long-short, um para cada família de indicadores. Estes portfolios são combinados para a criação de um portfolio final LS1. Os pesos negativos podem ser forçados para zero, e o portfolio redimensionado para que a soma dos pesos seja igual a 1. Neste caso, obtem-se um portfolio LO. Finalmente, utiliza-se um sistema proprietário, que é um modelo tático sistematico que varia a alocação entre os portfolios LO e LS, e portanto varia a exposição bruta e líquida do portfolio, a partir do ambiente macroeconômico do Brasil e do exterior, para produzir um portfolio LB (long-biased).
1 O rebalanceamento é feito mensalmente.
No caso dos métodos de aprendizagem de máquina, os indicadores são transformados diretamente em um portfolio LS, sem a criação de portfolios por família. Estima-se os retornos esperados de todas as ações para o próximo mês, e cria-se posições long para as ações com os 20% maiores retornos esperados, e short para as ações com os 20% menores retornos esperados. A partir daí, a metodologia é a mesma que no caso tradicional.
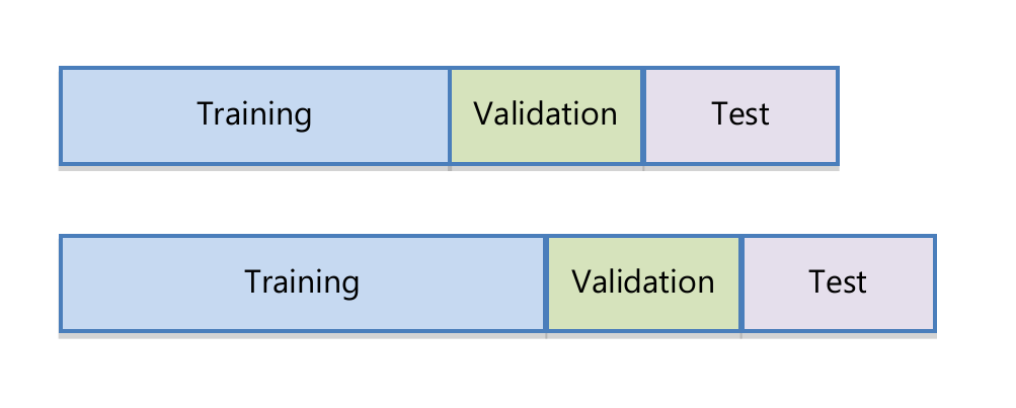
A estimação dos modelos de aprendizagem de máquina é feita com uma janela que se expande a cada mês. Seguindo Rubesam (2019), considera-se uma janela inicial de 24 meses como dados de treinamento. A partir daí, utiliza-se os próximos 12 meses para estimação dos hiperparâmetros (dados de validação), e então utiliza-se o modelo estimado (incluindo parâmetros e hiperparâmetros) para os 12 meses subsequentes (dados de teste). Esta janela se expande à cada 6 meses. O processo é ilustrado na Figura 4.
Seguindo Rubesam (2019), os retornos mensais e também os indicadores são transformados em rankings padronizados no intervalo (-1,1). Isto reduz a influência de outliers e faz com que a estimação seja mais robusta.
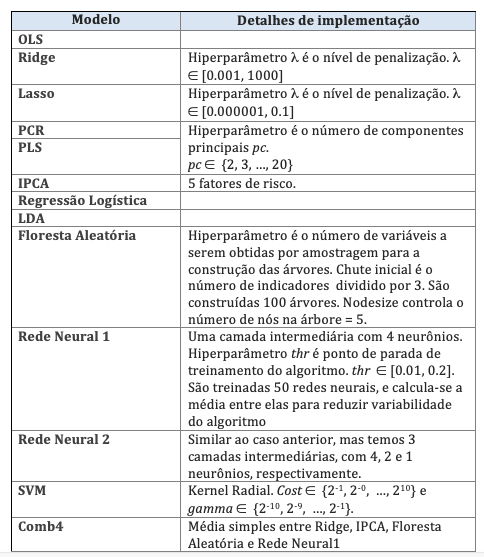
Consideramos seis modelos lineares: OLS (ordinary least squares), regressão ridge, regressão LASSO, PCR, PLS e IPCA. Adicionalmente, considera-se três modelos não-lineares: floresta aleatória e duas arquiteturas de redes neurais.
Também considera-se uma média simples de 4 modelos: regressão Ridge, IPCA, floresta aleatória e a rede neural mais simples. Este modelo combinado é denominado como “Comb4”.
Alguns detalhes de implementação são exibidos na Tabela 3. Toda a implementação foi em R, utilizando diversos pacotes, como ‘glmnet’, ‘pls’, ‘caret’, ‘randomForest’, ‘plm’ e ‘neuralnet’. O modelo IPCA foi implementado em Matlab.
5. Resultados
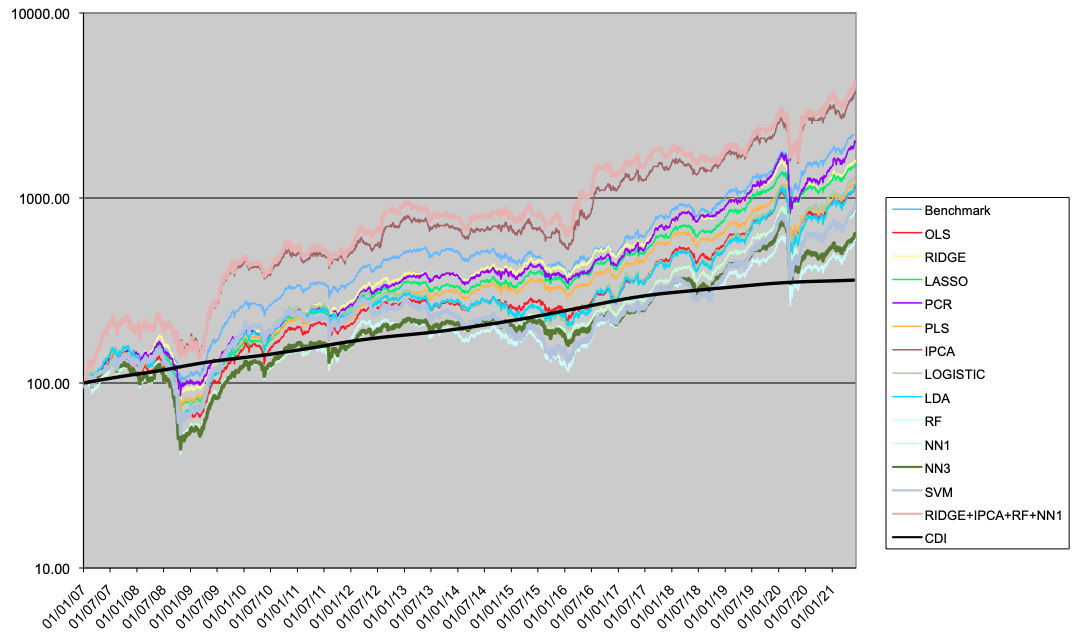
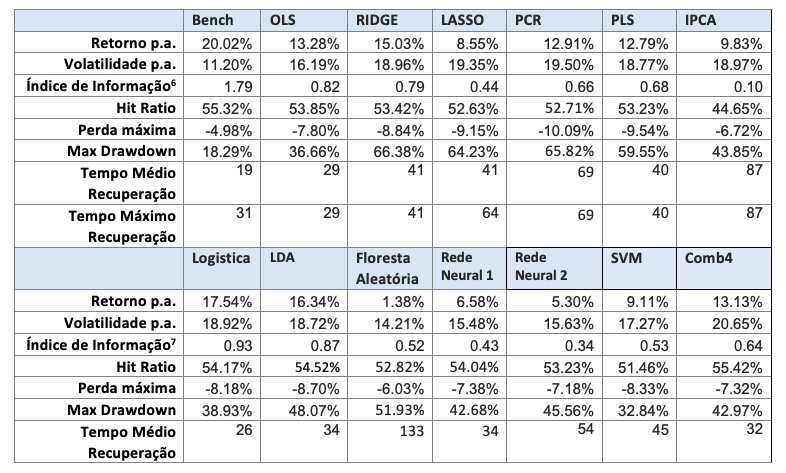
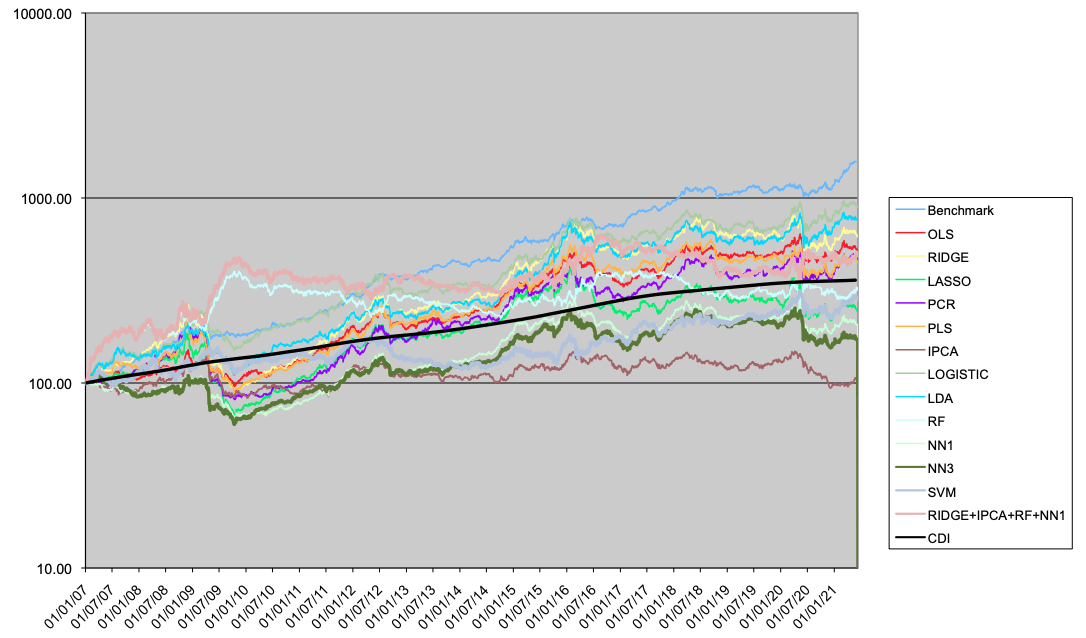
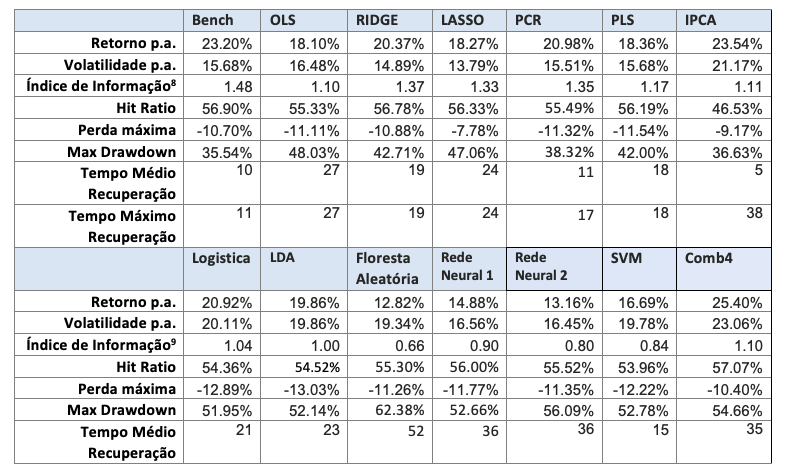
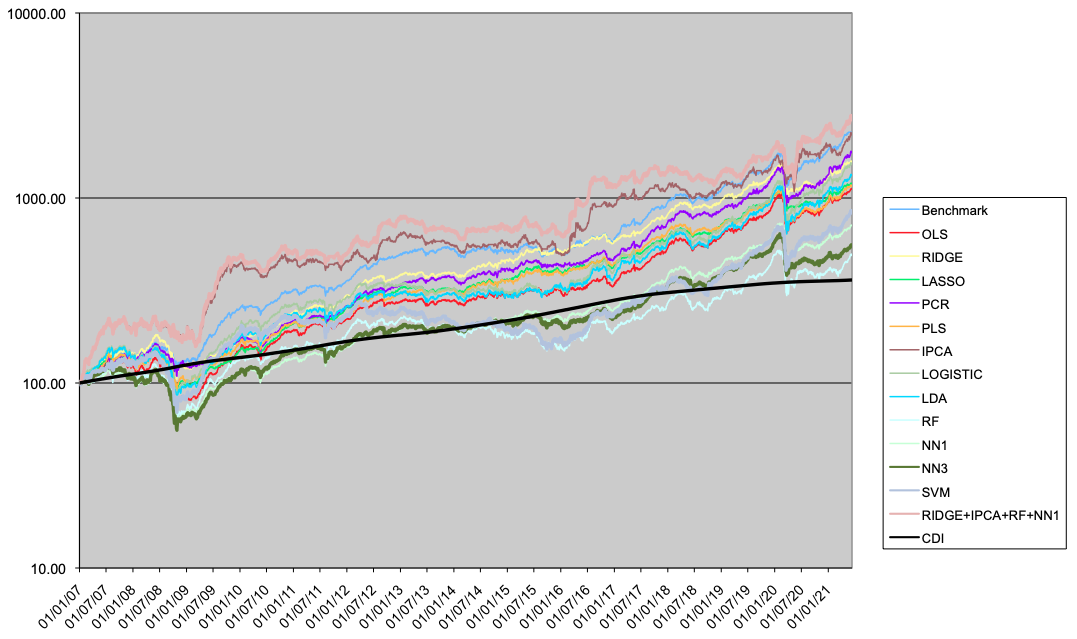
A seguir são apresentados os resultados para os portfolios LO (Tabela 4 e Figura 5), LS (Tabela 5 e Figura 6) e LB (Tabela 6 e Figura 7).
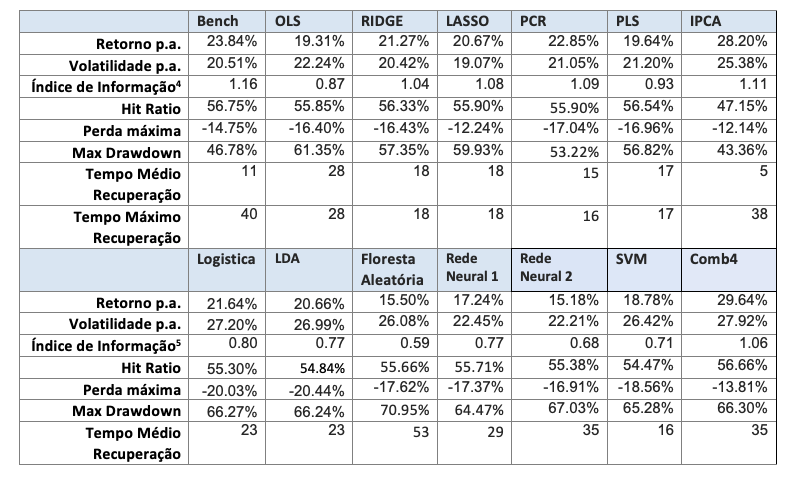
No caso long-only, os modelos lineares em geral têm resultados melhores que os não-lineares. Dois modelos superam o benchmark, o modelo IPCA, e o modelo Comb4. Estes dois modelos superam o benchmark tanto em Índice de Informação como em perfil de drawdown e tempo máximo de recuperação. Em relação aos modelos lineares, o uso de métodos de regularização (como Ridge ou PCR) tende à melhorar a performance em relação ao modelo OLS.
No caso long-short, nenhum modelo chega sequer próximo do Benchmark. Dentre os modelos alternativos, nota-se uma boa performance do Ridge, da Regressão Logística e da LDA.
Considerando o caso long-biased, que é a combinação das estratégias LO e LS conforme o modelo tático de alocação macro, os resultados dos modelos alternativos lineares superam os modelos não-lineares, mas não o benchmark. Ridge, PCR, IPCA e Comb4 são os melhores modelos alternativos em performance, sendo Ridge o melhor em termos de drawdown.
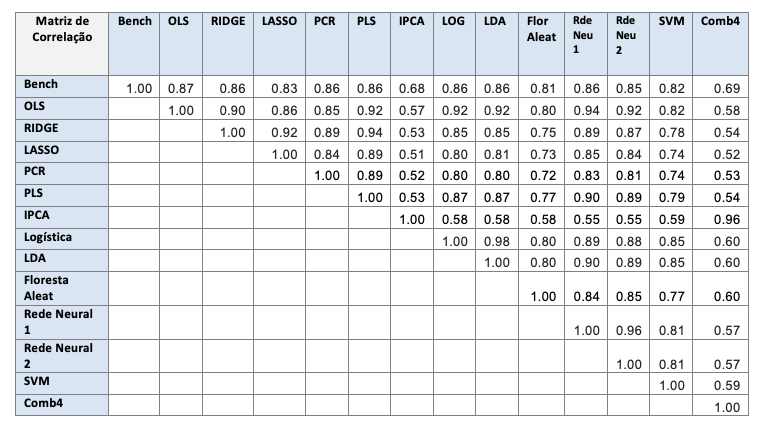
A Tabela 7 mostra a correlação entre os portfolios LB. Os modelos lineares têm correlação razoavelmente alta entre si, exceto com o IPCA, que funciona de maneira completamente diferente dos outros modelos. As correlações entre os modelos não-lineares também é alta. Os modelos IPCA e Comb4 têm a menor correlação com o benchmark.
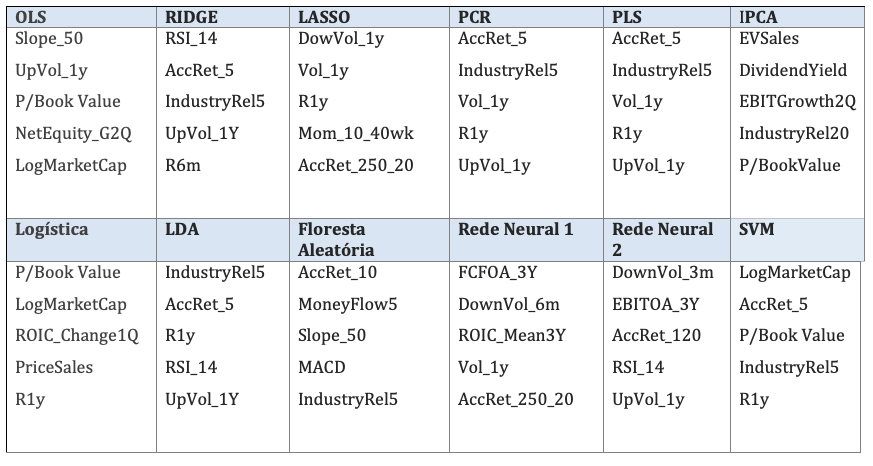
A Tabela 8 mostra as cinco variáveis mais importantes em cada modelo, obtidos out-of-sample. Observa-se que indicadores técnicos predominam na maioria dos modelos, exceto no modelo IPCA, onde predominam os indicadores fundamentalistas.
4. O índice de informação é obtido dividindo-se o retorno médio anualizado pela volatilidade anualizada, diferindo assim do índice de Sharpe, que deduz o retorno de um ativo livre de risco.
6. Conclusão
Foram testados diversos modelos alternativos para construção de portfolios de ações no mercado brasileiro. Os portfolios construídos foram long-only, long-short e long-biased. Foram considerados 5 modelos lineares, 3 modelos não-lineares, e uma combinação de 4 modelos.
Os resultados mostram que no caso de portfolios long-short, o método tradicional de construção de portfolios não é superado pelos modelos alternativos. Já nos casos long-only e long-biased, é justificado uma alocação experimental para modelos alternativos, sendo os principais candidatos o modelo IPCA, os modelos lineares com penalização, ou a combinação de 4 modelos. Visto que o modelo IPCA tem mais interpretabilidade e fundamentos teóricos, acredita-se que seja o melhor candidato.
7. Referências
- Berskon, J. (1944), “Application of the logistic function to bio-assay”, Journal of the American Statistical Association, 39, 357-365.
- Bishop, C.M. (1995) “Neural networks for pattern recognition”. Oxford university press.
- Breiman, L., Friedman, J., Olshen, R. and Stone, C. (1984) “Classification and regression trees”, Wadsworth, New York.
- Breiman, L. (2001) “Random forests”, Machine Learning, 45, 5-32.
- Carhart, M. (1997), “On persistence in mutual fund performance”, , 52 (1), 57-82.
- Cochrane, J. (2011), President address: Discount rates.
- Fama, E. F. e French, K. R. (1993), “Common risk factors in the returns on stocks and bonds”, Journal of Financial Economics 33(1), 3–56
- Fisher, R. A. (1936), “The use of multiple measurements in taxonomic problems”, Annals of Eugenics, 7: 179-188.
- Gu, S., Kelly, B. e Xiu, D. (2020), “Empirical asset pricing via machine learning”, The Review of Financial Studies 33 (5), 2223-2273.
- Gu, S., Kelly, B. e Xiu, D. (2021), “Autoenconder asset pricing models”, Journal of Econometrics 33 (5), 2223-2273.
- Hastie, T., Tibshirani, R. e Friedman, J.H. (2009) “The elements of statistical learning: data mining, inference, prediction”, Second Edition, Springer Verlag, 2009.
- Kelly, B., Pruitt, S. and Su, Y., (2019). “Characteristics are covariance: a unified model of risk and return”, Journal of Financial Economics, 134 (3), 501-524.
- Lintner, J. (1965) “The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets”, Review of Economics and Statistics, 47, 13-37.
- Markowitz, H. M. (1952) “Portfolio selection”, Journal of Finance, 7, 77-91.
- Mossin, J. (1966) “Equilibrium in a capital asset market”, Econometrica, 34, 768-783.
- Ripley, B. D. (1996) “Pattern recognition and neural networks”. Cambridge University press.
- Ross, S. (1976) “The arbitrage theory of capital asset pricing”, Journal of Economic Theory, 13 (3), 341-360.
- Rubesam, A. (2019) “Machine learning portfolios with equal risk contributions”, Working paper, IÉSEG school of management.
- Sharpe, W. (1964). “Capital Asset Prices: A Theory Of Market Equilibrium Under Conditions Of Risk,” Journal of Finance, 19 (3), 425-442.
- Vapnik, V. (1996), “Statistical Learning Theory”, Wiley, New York.